Предлагаем условия и авторские решения задач районной олимпиады 2009/2010 года, добавляя, как обычно, и свои пять копеек.

Задачи

По 5 баллов за каждую задачу. Если решение правильное, но ответ неверный: не более 3 баллов. За неправильное количество значащих цифр в ответе отнимается 1 балл. За отсутствие единиц измерения в ответе также отнимается 1 балл.

1.   Звезда Ахернар (а Эридана) наблюдалась в верхней и нижней кульминациях на высотах h₁ = 70°35' и h₂ = 5°03' над горизонтом соответственно. При этом обе кульминации происходили к югу от зенита. Пренебрегая рефракцией, определите географическую широту точки наблюдения.

Поскольку обе кульминации происходят к югу от зенита – наблюдатель находится в южном полушарии. Широту найдем из системы уравнений:

h₁=|φ|+90⁰+δ,

h₂=|φ|–90⁰–δ,

откуда

|φ|= (h₁+ h₂)/2=37⁰49’→ φ=–37⁰49’

Пять копеек.

В системе перепутаны знаки. Надо:

h₁=|φ|+90⁰–δ,

h₂=|φ|–90⁰+δ

Несмотря на ошибку, дальше все правильно.

2.   На неизвестной землеподобной планете главная звезда системы может наблюдаться в зените на широтах от -53.9° до 53.9°. Определите наклон местной эклиптики к экватору планеты.

Поскольку местное солнце может наблюдаться в зените на широтах ±53.9°, наклон эклип­тики к экватору равен 53.9°.

3.   Вы находитесь на мысе Доброй Надежды (34°21' ю. ш.). Определите склонение геостационарного спутника, находящегося над вашим меридианом. Землю считайте шарообразной.

Найдем расстояние от центра Земли данного геостационарного спутника:

r=[GM/(4π²)∙(23.93333∙3600 c)²]^⅓=4.2148∙10⁴ км

Найдем склонение спутника, сделав подходящий чертеж:

δ=arcsin[R_Esin φ/(r²+R_E²–2rR_Ecos φ)^0.5]=5.57⁰

В выражениях выше φ — модуль широты.

Пять копеек.

По определению: Геостационарный спутник - спутник, который располагается на высоте 35786 км (от центра Земли 42164 км) над экватором и обеспечивает непрерывность передачи данных. Расстояние до него определяется из формулы:

mv²/r=GmM/r²

С учетом того, что скорость:

v=2πr/T

r=[GMT/(4π²)]^⅓

С учетом T = 23^h56^m = 23,93333^h = 23,93333∙3600 с, должно выйти 4,2164∙10⁴ км. У нас получилось чуть меньше, но это не важно.

Далее делаем «подходящий» рисунок: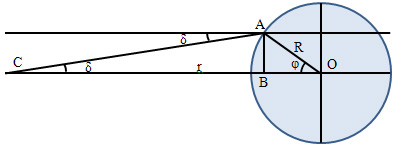

Спутник находится в точке C. Мы – в A. У нас два прямоугольных треугольника с общим катетом AB. Получим

AC sin δ = R sin φ

По теореме косинусов:

AC = (r²+R²–2rR cos φ)^0.5

(r²+R²–2rR cos φ)^0.5 sin δ = R sin φ

И далее как в решении.

4.   Годичный параллакс тройной звездной системы а Центавра равен 0.7421". Определите расстояние до системы в пк.

Расстояние до системы

r=1/0.7421” пк = 1.348 пк

Пять копеек.

На всякий случай:

r=1/π” пк

5.   Звезда α Центавра В обращается с периодом Р = 79.24 лет и большой полуосью a = 17.59" относительно звезды α Центавра А. Пренебрегая массой α Центавра С и используя значение параллакса системы из условия предыдущей задачи, вычислите сумму масс звезд А и В в массах Солнца.

Согласно третьему закону Кеплера, если период выражен в годах, большая полуось в а. е., масса в массах Солнца, можем записать:

M_A+M_B=(a/p)³/P²=2.12 M_☼

Пять копеек.

Большая полуось в условии дана в секундах дуги, но обозначена латинской буквой a, а не α (альфа). Вообще, условие очень запутано и некрасиво – альфа Центавра, альфа – угол, а – большая полуось. Период обозначается буквой P. В решении путаница продолжается: годичный параллакс (π), обозначается как горизонтальный (p), третий обобщенный закон Кеплера называется просто третьим законом Кеплера. Попробуем немного прояснить ситуацию.

Третий обобщенный закон Кеплера: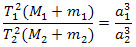

Если для Земли все значения брать равными единице, получим:

T²(M_A+M_B)=a³

Выразим сумму масс:

M_A+M_B=a³/T²

У нас T = P.

a найдем из рисунка: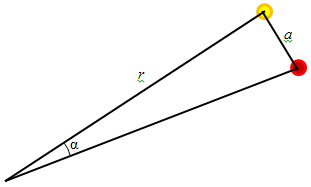

a = α∙r = α/π

Тогда:

^{Продолжение следует...}