Познакомился с заданиями 3 этапа РТ 2012 года. Среди "авторских" заданий мне не очень понравились две: В1 и В6. Приведу условия и решения этих задач:

В1.  Два грузовика по прямой дороге перевозят грузы из города A в город Б. В момент начала отсчета времени, грузовики выехали из разных городов навстречу друг другу. Зависимости модулей перемещений ∆r от времени t представлены на рисунке. Промежуток времени  ∆t с момента их первой встречи до второй равен … мин.

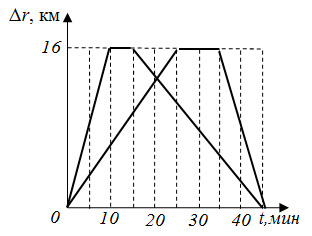
Решение: Если за точку отсчета принять город А, а за направление АВ, то уравнения движения машин на первом переезде из города в город будут следующие:

x1=v1 t;  x2=16-v2 t (км)

Где скорости легко находятся из графика:

 v1= 1,6 км/мин,  v1= 0,64 км/мин 

В момент первой встречи (как и другой) координаты машин будут равны:

 v1 t1=16-v2 t1 

Тогда  t1= 7,14 мин.

Время второй встречи я рассчитал, рассматривая движение в обратном порядке. Т.е. рассчитал время, которое проехали машины после их второй встречи до конца движения. Это удобно, ведь обе машины приехали домой через 45 мин после старта. Тогда:

u2 t' = 16 - u1 t'

Из графика, скорости машин на последних участках равны:

u2 = 1,6  км/мин,   u1 = 8/15  км/мин 

t' = 7,5 мин, а t2= 45 - 7,5 = 37,5 мин.

Время между встречами:

 ∆t= t2- t1=  37,5 мин - 7,14 мин = 30,36 мин.

Сразу приведу и следующую задачу. 

В6. Тепловой двигатель работает по циклу, изображенному на рисунке. Рабочим телом двигателя является идеальный одноатомный газ. Коэффициент полезного действия η этого двигателя равен … %.

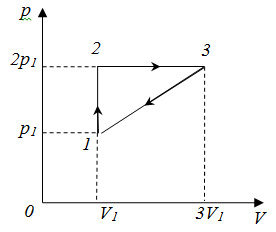
Решение:

КПД равно отношению полезной работы к затраченной. Полезная работа равна площади фигуры, ограниченной графиками:

А пол = p1 V1

Затрачена у нас теплота, переданная газу за цикл. Причем теплота передавалась в двух процессах:

Q = Q1 + Q2

Q1 =  ∆U1

Q1 =  ∆U2 + A2

∆U1 =  3/2 ∆p V1 =   3/2 p1 V1

∆U2 =  3/2 p2  ∆V =  6 p1 V1

A2 =  4 p1 V1

Итого:

Q = ∆U1 + ∆U2 + A2 = 11,5  p1 V1

Тогда КПД =  p1 V1/( 11,5  p1 V1 )*100% = 8,696%

Ну вроде ничего криминального - задачи решаются, все хорошо. Но здесь есть отход от традиции, которую сами авторы ЦТ и установили: обычно, ответы на задачи в части В очень близки к целым числам. Не помню, чтобы ответы отличались от целого значения более, чем на 0,15. В приведенных задачах ответы далеко не целые числа. Один ответ близок к 30,5 более, чем к 30; другой - к 8,5 ближе, чем к 9. Это наверняка сбило тестируемых, которые уже привыкли играть по правилам РИКЗ. Но как видим, ничто не вечно под Луной.