Начало...

Разные сантиметры. Эпизод 1

Рис. 53, стр. 44

На одном рисунке представлены мерная лента и линейка. Но шкалы у них разные: на 13 см мерной ленты укладывается 12,5 см линейки (с учетом начального отступа линейки).

Правильные и неправильные формы

В §10 часто упоминаются правильные формы. Начинается все со следующей проблемы:

Рис.56, стр. 45, §10

Цитата: «Представим себе, что в кружке авиамоделирования при создании модели самолета нужны три пластинки определенной площади (рис. 56), вырезанные из листа алюминия. Чтобы выбрать для этого лист алюминия, надо знать площади пластинок».

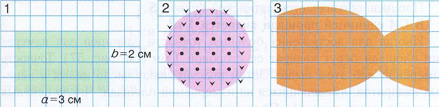
Рис.56

Все-таки, чтобы выбрать лист алюминия, надо знать не столько площадь, сколько форму и размеры пластинок. Но на этом разговор не заканчивается.

Стр. 47

Цитата: «Если пластинка правильной формы (см. рис. 56, пластинка 1), то площадь ее поверхности определяется просто: измеряют длину каждой из сторон пластинки (а и b). Площадь определяют по формуле

S = a·b…»

Обычно, про правильные формы говорят на конкурсе красоты. А на рис.56 какая фигура правильной формы? Трудно сказать, что имеют в виду под правильными формами авторы учебника, но я бы поставил на пластинку 2 – круг фигура правильная. С какой стати прямоугольник имеет правильные формы в данном случае не ясно.

Далее, вопросы к параграфу.

Стр. 48. Подумайте и ответьте

1. Как определить площадь поверхности правильной фигуры?

2. Каким способом определяется площадь поверхности неправильной фи­гуры?

А в здесь уже не правильные и неправильные формы, а фигуры. В данном случае речь идет о плоских фигурах, несмотря на некорректную постановку вопроса – можно подумать, что имеются в виду пространственные фигуры, и надо найти их площади поверхности. Из математики известно, что правильной будет та фигура, у которой все углы и все стороны равны. Круг также можно считать правильной фигурой. Но не прямоугольник, как в учебнике. 

Но и это не все.

Стр. 54. Подумайте и ответьте

1. Как определить объем тела правильной формы? Неправильной формы?

Могу предположить, что надо поучаствовать все же в конкурсе красоты.

Как Левша блоху подковал

Стр. 48. Сделайте дома сами

2. Изобразите в тетради квадрат площадью S₁ = 1 дм², внутри него — квадрат площадью S₂ = 1 см², внутри этого квадрата  —  квадрат площадью S₃ = 1 мм². Во сколько раз площадь S₁ больше площади S₂; площадь S₃ меньше площади S₁?

Трудно нарисовать квадрат площадью S₃ = 1 мм². Толщина сторон будет сопоставима с расстоянием между ними. Поэтому сделать это можно только с очень большой погрешностью. Я думаю, с этим заданием прекрасно справился бы Левша.

Разные сантиметры. Эпизод 2

Рис. 59, стр. 49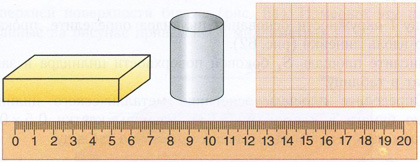

У бумаги с миллиметровыми делениями толстые квадраты имеют сторону 1 см. Глядя на линейку, можно заметить, что на расстоянии 4,5 см по линейке укладывается 5 см бумаги. Вот такие измерения.

Параллельность

Рис. 64, стр. 51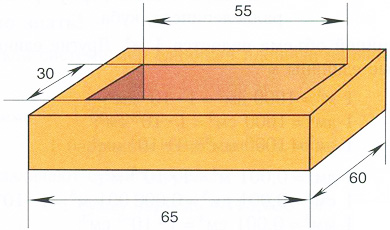

Не надо обладать супер зрением, чтобы заметить: линии, которые должны быть параллельны – ребра боковых стен, на самом деле далеко не параллельны. И тогда вычислить площадь верхней поверхности бруска нельзя. Кроме того не похоже, что толщина передней и задней стен в три раза больше, чем боковых, как указано на рисунке. Возможно, надо учитывать перспективу, но и тогда задняя часть стены не может быть толще передней. Если же рисунок правильный, тогда верхняя поверхность не лежит в одной плоскости! Кстати, такое же задание было и в рабочей тетради для 6 класса, по которой дети учились до этого, но рисунок там был более точный (хоть и черно-белый).

Волшебная гиря

Рис. 66, стр. 53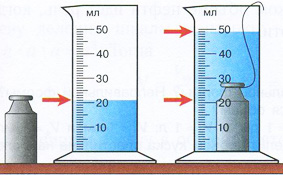

Основание гири в два раза меньше диаметра мензурки. Высота гири равна высоте вытесненной воды (даже чуть меньше). Как такое может быть? Даже если предположить, что гиря цилиндрическая, ее объем будет в 4 раза меньше (по моим подсчетам, с учетом формы гири, в 5 раз), чем объем вытесненной ей воды.

В продолжение темы

Рис. 69, стр. 55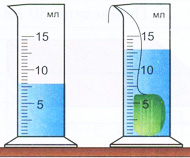

И на этом рисунке, смею предположить, объем пластилина значительно меньше вытесненной им воды (5 мл).

Стр. 54. Сделайте дома сами

Используя изготовленную вами мензурку, измерьте объем клубня картофеля. Определите точность ваших измерений.

Перед тем, как использовать, надо эту мензурку изготовить.

Стр. 54. Пример решения задачи

На сколько делений поднимется вода в мензурке, цена деления шкалы которой С = 2,0 см³/дел, если в нее полностью опустить стальной кубик с длиной ребра a = 4,0 см?

Проведя небольшие расчеты, можно заметить, что минимальное расстояние между штрихами на мензурке будет менее 0,8 мм. Т.е. меньше миллиметра. Обычно в мензурках расстояние больше, так как на точность измерений влияет такое явление как смачивание.

Стр. 58. Повторим главное в изученном

• Основными единицами, в которых измеряются физические ве­личины в Международной системе единиц (СИ), являются:

1 м — единица длины;

1 кг — единица массы;

1 с — единица промежутка времени;

1 К (К — градус по шкале Кельвина) — единица температуры.

• Чтобы перейти от кратных единиц к основной, надо умножить значения величин на 10, 100, 1000, ... .

• Чтобы перейти от дольных единиц к основной, надо значения величин разделить на 10, 100, 1000, ... .

• Точность измерения объема зависит от цены деления шкалы изме­рительного прибора. Чем она меньше, тем точность измерения больше.

• Площадь поверхности прямоугольной формы можно определить по формуле:

S = ab.

• Площадь поверхности небольшого тела неправильной формы можно определить с помощью миллиметровой бумаги или бумаги в клетку.

• Объем тела, имеющего форму прямоугольного параллелепипе­да, можно определить по формуле:

V = abc = Sc.

• Объем тела неправильной формы можно определить с помо­щью мензурки.

То, что Кельвин – единица температуры, говорилось вскользь. У детей обязательно по тому поводу возникнут вопросы, так как ни на одном термометре Кельвинов не было. Может рано упоминать Кельвины, и если нет, то стоит хотя бы немного рассказать о температурных шкалах?

При разговоре о кратных единицах не мешало бы указать на единицы времени, как исключение.

И, наконец, авторы сделали правильные выводы о формах, указав конкретно прямоугольник и прямоугольный параллелепипед. Ну что ж, лучше поздно…

Стр. 68, §14. Тепловое расширение

Вода при температурах от 0˚С до 4˚С не расширяется, а сжимается. Не мешало бы в параграфе указать на это исключение, тем более, что дети в повседневной жизни с этим сталкиваются.

Удивительные кольца

Рис. 91, стр. 69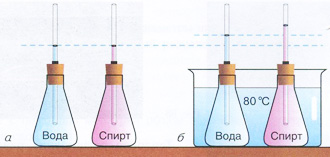

Начальные уровни воды и спирта на левом рисунке отмечены резиновыми кольцами. Интересно, что при нагревании эти кольца передвинулись вместе с уровнями жидкостей.

Рис. 105, стр. 78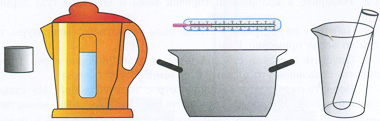

Среди оборудования для лабораторной работы вызывает интерес серый цилиндр слева. Что это? Ответить на этот вопрос нам поможет перечень оборудования в учебнике:

«Оборудование: калориметр, термометр, чайник с горячей водой и кастрюля (чайник) с водой комнатной температуры (одна на весь класс), стакан, пробирка (рис. 105)».

Методом исключения определяем – цилиндр не что иное как калориметр!?

Но это не все. Почти все объекты видны строго со стороны, и только стакан с пробиркой внутри под наклоном. Объекты делятся на цветные (чайник и термометр) и черно-белые (остальные). Возможно, этим указывается то, что в чайнике горячая вода. Кроме того, на чайнике нет кнопку включения, а крышка похоже больше на красную шапочку.

Стр. 78. Проверьте себя

«Почему нельзя измерять толщину листа линейкой?»

А почему нельзя? Можно, конечно. Нельзя ядовитые грибы есть, отравишься. А здесь измеряй, сколько хочешь, все равно ничего не получится.

Яблоки в ударе

Рис. 119, стр. 91. Сделайте дома сами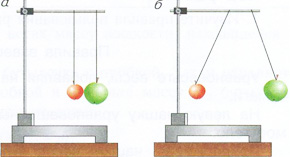

Подвесьте на нитях боль­шое яблоко и маленькое (рис. 119, а). Разведите нити с яблоками на некоторый угол (рис. 119, б) и отпустите. Заметьте, какое из яблок пос­ле удара отклонилось больше. Почему?

Наверное, в этом опыте лучше развести нити на одинаковые углы, а не на разные, как на рисунках. Кроме того, нити сильно растянулись, особенно левая. Яблоки не изменили своей ориентации, хотя по идее должны были повернуться на тот же угол, на который отклонились нити. А что будет после удара довольно интересно. Так как маленькой яблоко отклонили на больший угол, результат столкновения не совсем ясен. Яблоки вряд ли буду взаимодействовать абсолютно упруго, поэтому их кинетическая энергия частично или полностью перейдет в тепловую. Опыт может быть не слишком наглядным. Ну а где ученики возьмут дома штатив, представляет еще большую загадку.

Рис. 122, стр. 94.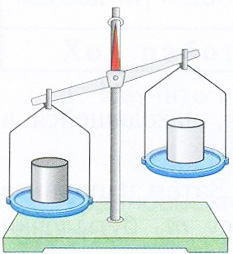

Похоже, весы сломались – несмотря на то, что они не в равновесии, красная стрелка не шелохнулась.

Стр. 98. Интересно знать

Уже при жизни знаменитого древнегреческо­го ученого Архимеда о нем слагались легенды, поводом для которых служили его изоб­ретения, поражавшие современников. Одна из легенд гласит, что сиракузский царь Герон II по­просил мыслителя …

Кое-где в Интернете действительно сиракузского тирана Гиерона (ударение на втором слоге) называют просто Герон. Но в солидных изданиях его именуют Гиерон Младший или Гиерон II, в отличие от знаменитого древнегреческого математика Герона.

Стр. 103. Это вы можете выполнить сами

1. Какие физические величины измеряют с помощью мензурки, ли­нейки, секундомера, спидометра, термометра, весов?     

2. Обоснуйте справедливость высказывания Леонардо да Винчи…

И дальше в том же духе. Все же здесь надо не выполнить, а ответить на вопросы.

Рис. 128, стр. 105.

26. На рисунке 128 изображен динамометр — прибор для измерения физической величины «сила». Сила изме­ряется в ньютонах (Н). Нижний предел измерения шкалы прибора F_H = О Н. Определите верхний предел измерения, цену деления шка­лы и показание динамометра.

Нижний предел измерения шкалы прибора не F_H = О Н, а 0,8 Н. Меньше измерить не позволит слишком маленькая длина основания крюка (красная стрелка). Расстояние, на которое может подняться указатель, соответствует значению не менее 0,8 Н.

Рис. 138, стр. 112.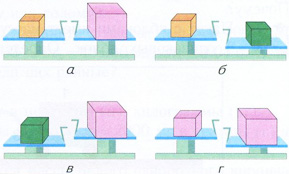

Более чем странные весы.

Стр. 103. Латинский алфавит

Не совсем полные названия латинских букв, так как многие из них можно читать не одним способом. Например, «Е» можно читать не только «э», но и «е», что и делают многие учителя. То же касается буквы «G» - читать можно не только «гэ», но и «жэ». «J» мы чаще читаем как «жи», а не «йот», а «Y» можно читать как «Ипсилон», а не только как «Игрек».